Thinking of Probabilities in Terms of Areas

This note describes an approach for intuitively understanding many facts of probability used throughout this set of notes.

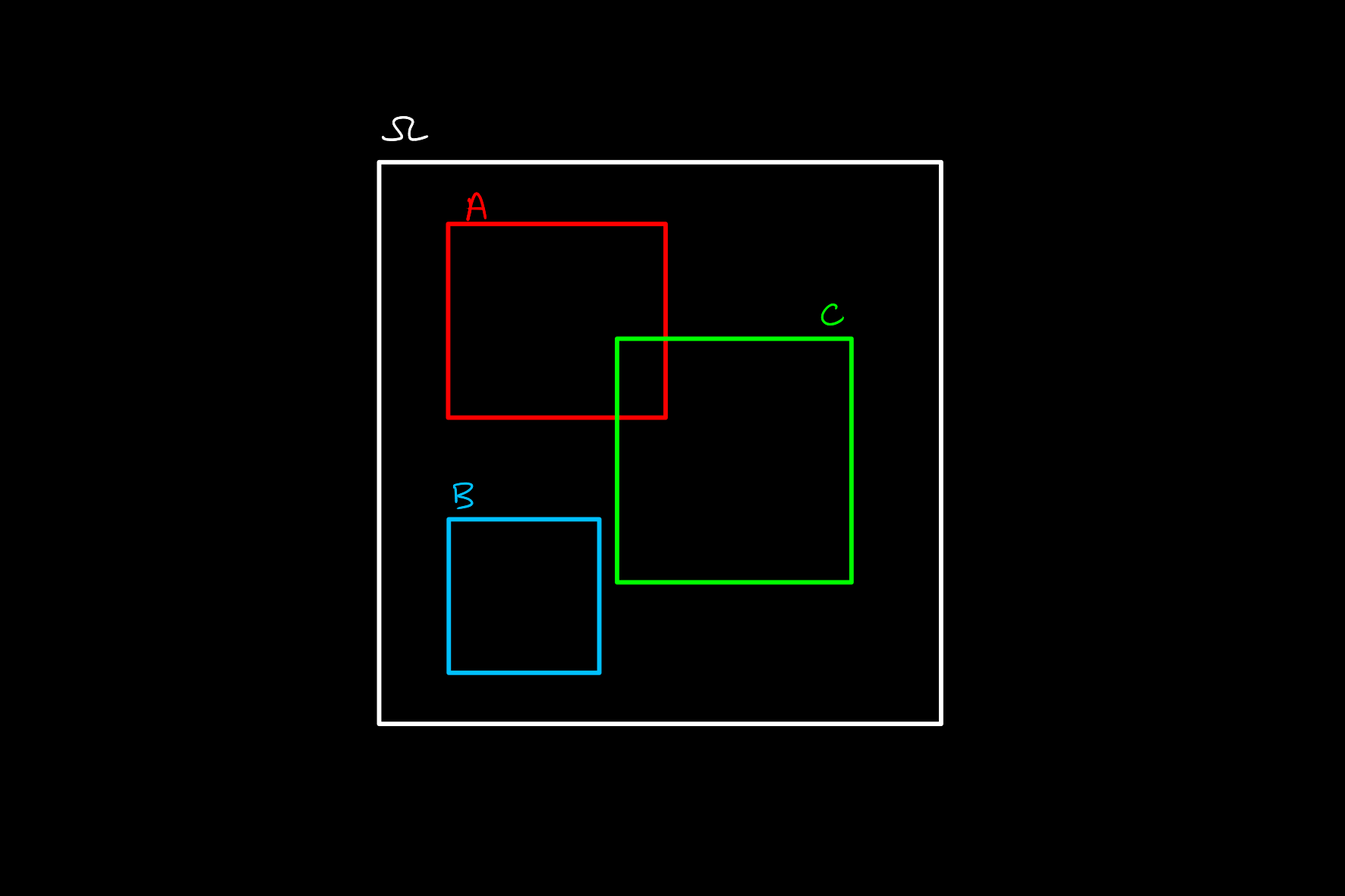
This approach is to consider the probability space \(\Omega\) to be a subset of \(\mathbb{R}^2\) with area \(1\). That is, we draw \(\Omega\) as a square (or rectangle) and then draw subsets of it within it.

We draw this diagram such that the probability of an event occurring is equal to the area that it takes up (as a proportion of the whole area).

Then thinking of and and or conditions on probabilities in terms of the intersection and union respectively, as well as conditional probability by viewing things relative to a subset of the whole space become obvious.

It is important to note that this way of thinking about probability is not just a visual trick, or a way to obscure what is going on. Ultimately, this is just working with a particular probability space which is a subset of \(\mathbb{R}^2\), with the Lebesgue measure used as a probability function.

Example

A classic example of a question in probability which is made significantly simpler by considering it in this way is with problems related to Bayes' theorem.

Consider the following problem:

Example

It is known that \(1\%\) of individuals have a particular disease. It is also known that:

  1. Given a person is positive, they have a \(90\%\) change of testing positive (sensitivity).
  2. Given a person is negative, they have a \(90\%\) change of testing negative (specificity).

What is the probability that in individual has the disease, assuming they have tested positive?

The answer in this case (found by applying the law of total probability and bayes' theorem is \(\frac{1}{100}\)):

\[\begin{align*} P(D \mid T) &= \frac{P(T \mid D)P(D)}{P(T)} \\ &= \frac{P(T \mid D)P(D)}{P(T \mid D)P(D) + P(T \mid D^c)P(D^c)} \\ &= \frac{0.9 \times 0.01}{0.9 \times 0.01 + 0.9 \times 0.99} \\ &= \frac{1}{100} \\ \end{align*}\]

This is a result that often seems unintuitive to many people at first glance.

However by drawing up a probability space and representing the probabilities of events by areas, we can clearly see why this is true.

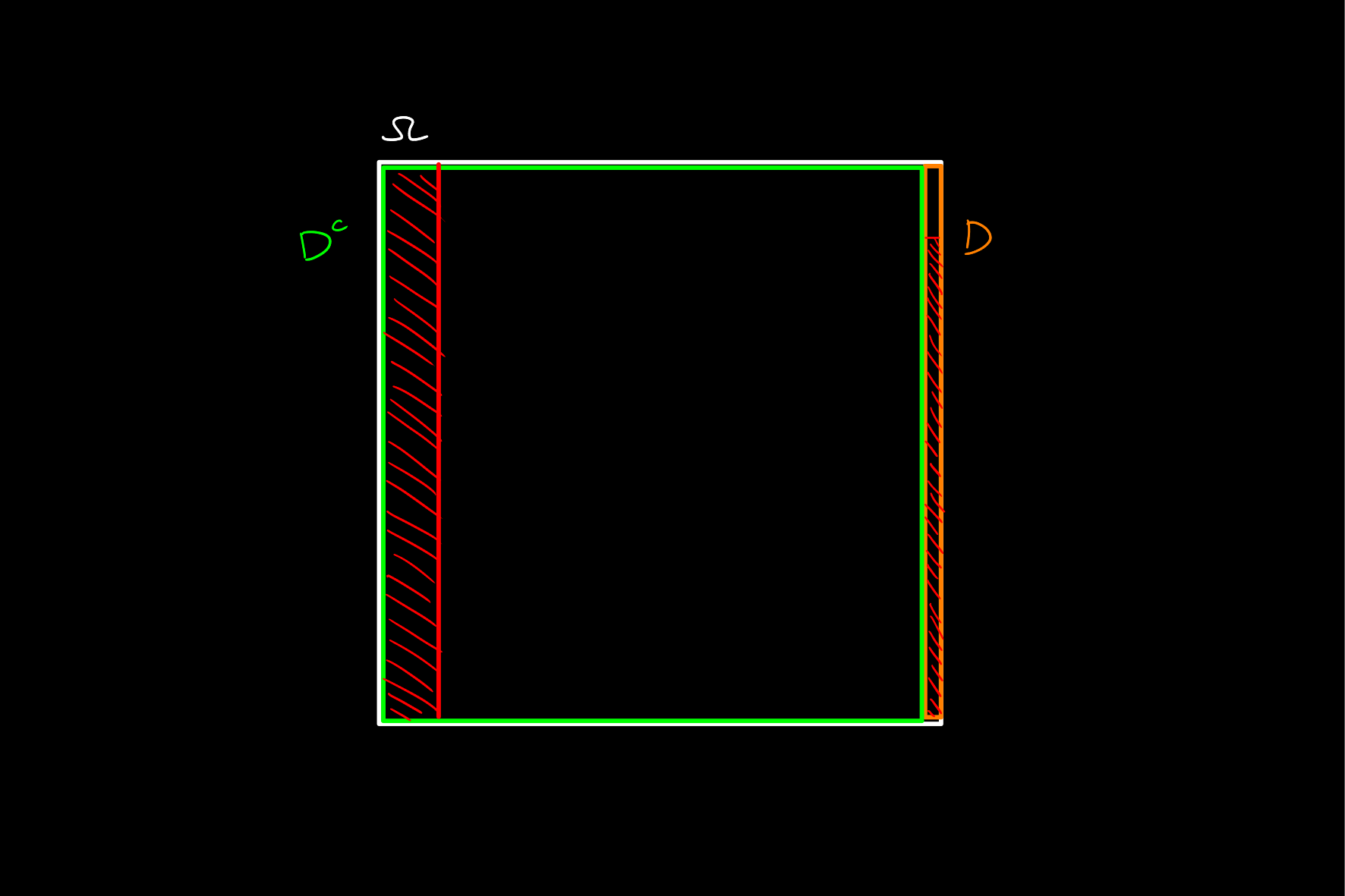
Note the below diagram where the probability of having the disease and not having the disease are shown:

And now, by colouring in the probability of a positive test in both of these cases as the corresponding proportion of each of these areas, it becomes obvious why given a positive test, it is still way more likely that you are not infected: